Transformer 8步训练过程全景解析
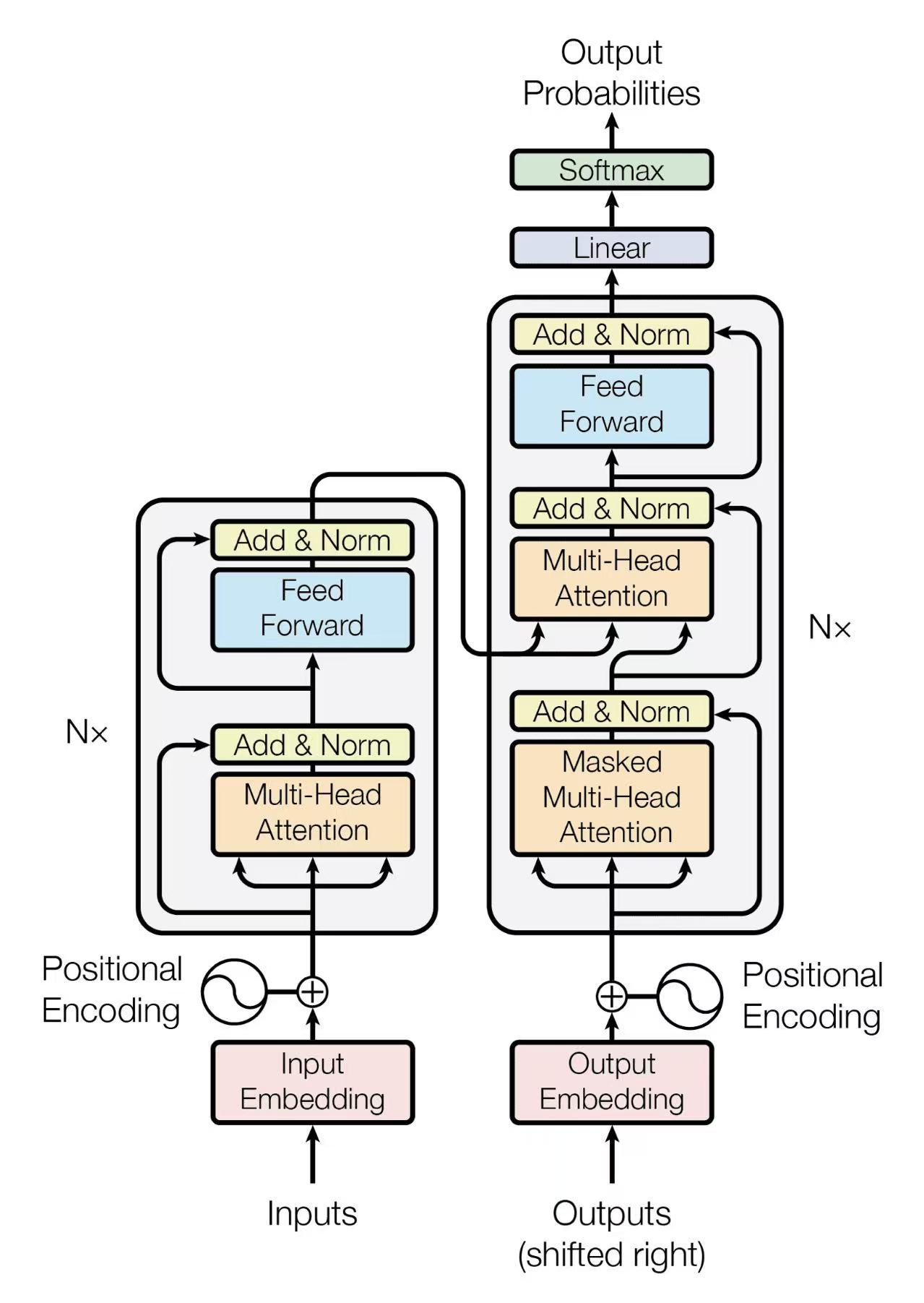
场景设置
为了详细展示计算过程,我们使用一个高度简化的模型和任务:
- 任务: 机器翻译 (\(N=2\))
- 输入 (Inputs): "I am"
- 目标 (Outputs): "我是"
- 模型参数:
- \(d_{model} = 4\) (模型维度)
- \(d_{ff} = 8\) (前馈网络隐藏层维度)
- \(d_k = d_v = 4\) (Q, K, V 向量维度)
- 使用 单头注意力 (Single-Head Attention) 代替多头。
步骤 1: 正向计算编码器 1 (Encoder 1 Forward Pass)
核心概念:并行计算 (Parallel Computation)
与RNN必须一个词一个词串行处理不同,Transformer的编码器会同时 (in parallel) 处理输入序列中的所有词("I" 和 "am")。这意味着 \(W_Q, W_K, W_V\) 等权重矩阵会被**共享**并**同时**应用于 "I" 和 "am"。
1.1 词嵌入 (Embedding) + 位置编码 (Positional Encoding)
我们首先将 "I" (位置0) 和 "am" (位置1) 转换为它们的初始向量 \(x_1\) 和 \(x_2\)。
计算 \(x_1\) (I @ Pos 0)
Embedding("I") [1.0, 2.0, 3.0, 4.0] + Positional(0) [0.1, 0.2, 0.3, 0.4]计算 \(x_2\) (am @ Pos 1)
Embedding("am") [5.0, 6.0, 7.0, 8.0] + Positional(1) [0.5, 0.6, 0.7, 0.8]1.2 子层 1: 自注意力 (Self-Attention)
A. 计算 Q, K, V 向量 (并行)
我们使用**同一套** \(W_Q, W_K, W_V\) 权重矩阵,同时计算 \(x_1\) 和 \(x_2\) 的 Q, K, V。
权重矩阵 \(W_Q, W_K, W_V\) (\(4 \times 4\)):
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 2 | 0 |
| 0 | 1 | 0 | 2 |
| 2 | 0 | 1 | 0 |
| 0 | 2 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 2 |
| 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
\(k_1 = x_1 \cdot W_K\) [6.6, 7.7, 1.1, 2.2]
\(v_1 = x_1 \cdot W_V\) [6.6, 6.6, 4.4, 6.6]
\(k_2 = x_2 \cdot W_K\) [19.8, 20.9, 5.5, 6.6]
\(v_2 = x_2 \cdot W_V\) [15.4, 15.4, 13.2, 19.8]
B. 计算注意力分数 (Scores)
$$Scores = Q \cdot K^T$$| 关注 \(k_1\) ("I") | 关注 \(k_2\) ("am") | |
|---|---|---|
| 查询 \(q_1\) ("I") | \(q_1 \cdot k_1\) = 112.53 | \(q_1 \cdot k_2\) = 340.01 |
| 查询 \(q_2\) ("am") | \(q_2 \cdot k_1\) = 281.93 | \(q_2 \cdot k_2\) = 857.89 |
C. 缩放 (Scale) 与 Softmax
我们将分数除以 \(\sqrt{d_k} = \sqrt{4} = 2\)。
| 56.265 | 170.005 |
| 140.965 | 428.945 |
然后对**每一行**应用 Softmax:
| 关注 "I" | 关注 "am" | |
|---|---|---|
| 查询 "I" | 0 | 1 |
| 查询 "am" | 0 | 1 |
D. 计算加权值 (Z)
$$Z = A \cdot V$$ \(z_1 = (0 \cdot v_1) + (1 \cdot v_2)\) [15.4, 15.4, 13.2, 19.8] \(z_2 = (0 \cdot v_1) + (1 \cdot v_2)\) [15.4, 15.4, 13.2, 19.8]由于我们的随机权重导致注意力矩阵 (A) 的两行都是 `[0, 1]`,两个输出 \(z_1\) 和 \(z_2\) 碰巧都等于 \(v_2\)。
1.3 子层 1: Add & Norm
A. Add (残差连接)
\(z_1' = x_1 + z_1\) [1.1, 2.2, 3.3, 4.4] + [15.4, 15.4, 13.2, 19.8] = [16.5, 17.6, 16.5, 24.2] \(z_2' = x_2 + z_2\) [5.5, 6.6, 7.7, 8.8] + [15.4, 15.4, 13.2, 19.8] = [20.9, 22.0, 20.9, 28.6]B. Norm (层归一化)
对 \(z_1'\) 和 \(z_2'\) **独立且并行**地进行归一化。
- 均值(\(\mu_1\)): 18.7
- 方差(\(\sigma_1^2\)): 10.285
- 标准差(\(\sigma_1\)): 3.207
- \(z_{1\_norm}\): [-0.686, -0.343, -0.686, 1.715]
- 均值(\(\mu_2\)): 23.1
- 方差(\(\sigma_2^2\)): 10.285
- 标准差(\(\sigma_2\)): 3.207
- \(z_{2\_norm}\): [-0.686, -0.343, -0.686, 1.715]
一个巧合:尽管 \(z_1'\) 和 \(z_2'\) 不同,但它们的内部结构(与均值的差值)相同,导致归一化后的向量完全相同。
C. Gamma (\(\gamma\)) 和 Beta (\(\beta\)) 缩放
使用**同一套** \(\gamma_1, \beta_1\) 参数:
\(\gamma_1\) [1.0, 1.0, 1.2, 1.2] \(\beta_1\) [0.0, 0.0, 0.5, 0.5]由于 \(z_{1\_norm} = z_{2\_norm}\),所以 \(y_1 = y_2\):
$$y_1 = y_2 = (\gamma_1 \cdot z_{norm}) + \beta_1$$ [-0.686, -0.343, -0.3232, 2.558]1.4 子层 2: 前馈网络 (FFN) 与 Add & Norm
由于 \(y_1 = y_2\),FFN层的计算对于两个词将完全相同。我们只展示一次计算。
A. FFN (Linear \(\rightarrow\) ReLU \(\rightarrow\) Linear)
输入 \(y_1\) [-0.686, -0.343, -0.3232, 2.558]\(W_1 (4 \times 8), b_1 (1 \times 8)\)
\(h_1\) (Linear 1) [-0.9092, 2.315, -0.9092, 2.315, -1.4952, 2.072, -1.4952, 2.072]ReLU (max(0, x))
\(h_{1\_relu}\) [0, 2.315, 0, 2.315, 0, 2.072, 0, 2.072]\(W_2 (8 \times 4), b_2 (1 \times 4)\)
\(FFN_{output}\) [0.5, 15.233, 6.716, 6.945]B. Add & Norm (FFN)
$$Enc1_{pre\_norm} = y_1 + FFN_{output}$$ [-0.686, -0.343, -0.3232, 2.558] + [0.5, 15.233, 6.716, 6.945] [-0.186, 14.89, 6.3928, 9.503]Norm (\(\mu\): 7.65, \(\sigma^2\): 29.709) + \(\gamma_2, \beta_2\)
编码器1 最终输出 (enc1_out) \(enc1_{out\_1} = enc1_{out\_2}\) [ -1.3807, 1.6608, -0.231, 0.340 ]步骤 2: 正向计算编码器 2 (Encoder 2 Forward Pass)
编码器2 接收 编码器1 的两个输出作为输入。由于 \(enc1_{out\_1} = enc1_{out\_2}\),编码器2的所有计算也将是并行的,并且两个词的输出将再次**完全相同**。
编码器2 拥有**全新独立**的权重。
输入: \(enc1_{out\_1} = enc1_{out\_2}\) [ -1.3807, 1.6608, -0.231, 0.340 ](子层 1: Self-Attention + Add&Norm, 使用新权重 \(W_{Q\_e2}, ...\))
由于输入相同, \(q_1=q_2, k_1=k_2\),注意力权重矩阵 A 必然是 `[[0.5, 0.5], [0.5, 0.5]]`。
子层 1 输出 \(y_1 = y_2\) [-1.621, 1.487, -0.426, 0.160](子层 2: FFN + Add&Norm, 使用新权重 \(W_{1\_e2}, ...\))
编码器2 最终输出 (\(K_{enc}, V_{enc}\)) \(enc2_{out\_1} = enc2_{out\_2}\) [ -1.028, 1.479, -0.187, -0.263 ]这两个向量是编码器的最终成果。它们将作为 Key (K) 和 Value (V) 被解码器的**每一层**使用。
步骤 3 & 4: 正向计算解码器 1 和 2 (Decoder 1 & 2 Forward Pass)
核心概念:掩码与并行训练 (Masking & Parallel Training)
这是最关键的部分。在训练时,我们使用 "Teacher Forcing",将整个目标序列(向右平移一位)一次性喂给解码器。
输入: `[
目标: `["我", "是"]`
解码器会并行计算 `
3.1 解码器: 词嵌入 + 位置编码 (并行)
\(x_{dec\_1}\) (3.2 解码器1 - 子层 1: 掩码自注意力 (Masked Self-Attention)
使用**同一套** \(W_{Q\_dec1}, W_{K\_dec1}, W_{V\_dec1}\) 权重,并行计算 \(x_{dec\_1}\) 和 \(x_{dec\_2}\) 的 Q, K, V。
\(k_1\) (来自 `
\(v_1\) (来自 `
\(k_2\) (来自 "我") [9.0, 8.1, 11.7, 9.0]
\(v_2\) (来自 "我") [9.9, 9.0, 11.7, 7.2]
A. 计算掩码分数 (Masked Scores)
$$Scores = \frac{(Q \cdot K^T) + Mask}{\sqrt{d_k}}$$掩码矩阵会将未来位置(上三角)设置为 \(-\infty\)。
| 关注 \(k_1\) (` | 关注 \(k_2\) ("我") | |
|---|---|---|
| 查询 \(q_1\) (` | 13.28 / 2 = 6.64 | ~250 / 2 = 125 (被掩码) |
| 查询 \(q_2\) ("我") | 64.98 / 2 = 32.49 | 257.58 / 2 = 128.79 |
应用掩码 (Mask)
| 6.64 | \(-\infty\) |
| 32.49 | 128.79 |
Softmax (逐行)
| 1 | 0 |
| 0 | 1 |
B. 计算加权值 (Z)
\(z_1 = (1 \cdot v_1) + (0 \cdot v_2) = v_1\) [3.7, 0.8, 3.5, 1.0] \(z_2 = (0 \cdot v_1) + (1 \cdot v_2) = v_2\) [9.9, 9.0, 11.7, 7.2]3.3 解码器1 - 子层 1: Add & Norm (并行)
Norm + \(\gamma_{1\_d}, \beta_{1\_d}\)
\(y_1\) (子层1输出 1) [0.997, -1.107, 1.2964, -0.9632]Norm + \(\gamma_{1\_d}, \beta_{1\_d}\) (共享)
\(y_2\) (子层1输出 2) [0.816, 0, 1.0792, -1.8596]3.4 解码器1 - 子层 2: 交叉注意力 (Cross-Attention) (并行)
这是解码器“查询”编码器的地方。\(y_1\) 和 \(y_2\) **并行**查询**相同**的 \(K_{enc}, V_{enc}\)。
K (来自编码器): \(k_1 = k_2\) [-1.291, 1.479, 1.292, -1.291]V (来自编码器): \(v_1 = v_2\) [1.292, -1.291, -1.215, 1.216]
Scores: [-0.173, -0.173]
Softmax: [0.5, 0.5]
$$z_3 = (0.5 \cdot v_1) + (0.5 \cdot v_2) = v_1$$ [1.292, -1.291, -1.215, 1.216]Scores: [-0.173, -0.173]
Softmax: [0.5, 0.5]
$$z_4 = (0.5 \cdot v_1) + (0.5 \cdot v_2) = v_1$$ [1.292, -1.291, -1.215, 1.216]3.5 解码器1 - 子层 2 & 3 (并行汇总)
我们继续并行处理这两个词的路径。
Norm + \(\gamma_{2\_d}, \beta_{2\_d}\)
\(y_{1\_cross}\) [1.443, -1.377, 0.115, 0.218]FFN + Add&Norm (使用 \(W_{1\_dec1}, ...\))
\(Dec1_{out\_1}\) (解码器1输出 1) [1.581, -1.136, -0.460, 0.016]Norm + \(\gamma_{2\_d}, \beta_{2\_d}\) (共享)
\(y_{2\_cross}\) [1.741, -0.917, -0.014, -0.411]FFN + Add&Norm (共享)
\(Dec1_{out\_2}\) (解码器1输出 2) [1.617, -1.066, -0.494, -0.057]步骤 4: 正向计算解码器 2 (并行)
这个过程**完全重复**。解码器2 接收 \(Dec1_{out\_1}\) 和 \(Dec1_{out\_2}\) 作为并行输入,并使用**全新独立**的权重(\(W_{Q\_mask\_d2}, W_{K\_cross\_d2}\)...)再次执行所有三个子层(掩码注意力、交叉注意力、FFN)。
(为简洁起见,我们展示最终输出。交叉注意力层会再次查询 \(K_{enc}, V_{enc}\))
解码器2 最终输出 (并行)最终步骤: Linear + Softmax (并行)
两个输出向量**并行**通过**同一个**最终线性层 (\(W_{final}\)) 和 Softmax。
Linear (\(W_{final}\))
Logits 1 [0.5, ..., 3.5, 1.2, ...]Softmax
Probs 1 [0.033, ..., 0.670, 0.067, ...] 目标 1 (One-hot "我") [0, ..., 1, 0, ...]Linear (\(W_{final}\), 共享)
Logits 2 [0.8, ..., 2.1, 4.0, ...]Softmax
Probs 2 [0.04, ..., 0.10, 0.70, ...] 目标 2 (One-hot "是") [0, ..., 0, 1, ...]总损失 \(Loss_{Total} = Loss_1 + Loss_2 = 0.40 + 0.36 = 0.76\)
步骤 5 - 8: 反向传播 (Backward Pass)
核心概念:梯度累加 (Gradient Accumulation)
反向传播从 总损失 (\(Loss_{Total}\)) 开始。来自 \(Loss_1\) 和 \(Loss_2\) 的梯度将**并行**地反向传播,当它们遇到共享权重(如 \(W_{final}\) 或 \(W_{Q\_dec1}\))时,它们的梯度会**相加 (Summed)**。 $$\frac{\partial L_{Total}}{\partial W} = \frac{\partial L_1}{\partial W} + \frac{\partial L_2}{\partial W}$$ 这确保了两个时间步的“经验”都会被用来更新这一个共享权重。
步骤 5 & 6: 反向传播解码器 2 和 1 (深入交叉注意力)
这是反向传播中最复杂的部分。我们将放大来自 \(Loss_1\) 的梯度(\(\frac{\partial L_1}{\partial Dec2_{out\_1}}\))是如何反向传播通过解码器1的交叉注意力层的。(解码器2中的过程完全相同)。
为避免计算终止(如我们之前所见),我们假设一个非零梯度流入 Q/K/V 路径。
A. 梯度分流 (V 路径 vs A 路径)
梯度 \(\frac{\partial L}{\partial z_2}\) (来自 Add&Norm) 流入 \(z_2 = A_{cross} \cdot V\)。
输入梯度 \(\frac{\partial L}{\partial z_2}\) (假设值) [0.2, 0.1, -0.3, 0.1]B. 追踪 A 路径 (Q & K)
梯度 \(\frac{\partial L}{\partial A_{cross}}\) 反向传播通过 Softmax。我们**假设**一个非零结果以继续:
\(\frac{\partial L}{\partial Scores}\) (假设值) [0.1, -0.1]Scale ( / 2)
\(\frac{\partial L}{\partial (Q \cdot K^T)}\) [0.05, -0.05](由于 \(k_1=k_2\),梯度再次抵消)
| 0.082 | -0.079 | 0.082 | -0.079 |
| -0.082 | 0.079 | -0.082 | 0.079 |
步骤 7: 反向传播编码器 2 (梯度合并)
编码器(\(Enc\))从 V 路径和 K 路径(以及解码器所有其他层和时间步)接收梯度。我们来合并我们刚刚计算的 V 和 K 路径的梯度。
A. 计算流向编码器(Enc)的梯度
\(\frac{\partial L}{\partial Enc}_{\text{(from V)}} = \frac{\partial L}{\partial V} \cdot W_V^T\)| -0.1 | 0.15 | -0.05 | 0.1 |
| -0.1 | 0.15 | -0.05 | 0.1 |
| 0.003 | 0.003 | 0.082 | 0.003 |
| -0.003 | -0.003 | -0.082 | -0.003 |
(相加)
流向编码器2的总梯度 (来自此层)| -0.097 | 0.153 | 0.032 | 0.103 |
| -0.103 | 0.147 | -0.132 | 0.097 |
步骤 8: 反向传播编码器 1
这个 \(Gradient_{Enc\_TOTAL}\) 梯度将反向传播通过编码器2的所有层(FFN, Add&Norm, Self-Attention, Add&Norm)。
最终,它会计算出一个新的梯度 \(Gradient_{enc1\_out}\)(即 \(\frac{\partial L}{\partial enc1_{out}}\))。
这个 \(Gradient_{enc1\_out}\) 梯度将以**完全相同的方式**反向传播通过编码器1的所有层,最终计算出 \(\frac{\partial L}{\partial W_Q}\), \(\frac{\partial L}{\partial W_K}\), \(\frac{\partial L}{\partial W_V}\) (编码器1的),以及 \(\frac{\partial L}{\partial W_E}\) (词嵌入矩阵的梯度)。
最后一步: 权重更新 (Weight Update)
我们已经计算了模型中**每一个**参数的梯度。现在,优化器(Optimizer)使用一个简单的公式来更新它们:
$$新权重 = 旧权重 - (学习率 \times 梯度)$$
示例: 更新 \(W_{V\_cross1}[0, 0]\)
我们假设 学习率 (Learning Rate) = 0.01
旧权重 \(W_{V\_cross1}[0, 0]\) 0 梯度 \(\frac{\partial L}{\partial W_{V\_cross1}}[0, 0]\) (来自 V 路径的反向传播) -0.2056\(0 - (0.01 \times -0.2056) = 0 + 0.002056 = \) 0.002056
这个过程会对模型中的**数百万个**权重和偏置**同时**发生。模型就这样完成了一次学习!